» Магические квадраты
|
В данной части работы мы в основном следуем книге [2].
2.1 Первые магические квадраты.
Одним из наиболее древних и наиболее совершенных видов кросс-сумм является так называемый магический (или волшебный) квадрат.
Придуманы магические квадраты впервые, по-видимому, китайцами, так как самое раннее упоминание о них встречается в китайской книге, написанной за 4000—5000 лет до нашей эры.
Старейший в мире магический квадрат китайцев представлен на рисунке 2.0.
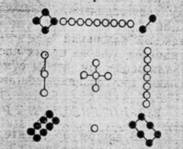
рисунок 2.0
Черными кружками в этом квадрате изображены четные (ж) числа, белыми – нечетные (м) числа. В обычной записи он не так эффектен.
1 |
14 |
15 |
4 |
12 |
7 |
6 |
9 |
8 |
11 |
10 |
5 |
13 |
2 |
3 |
16 |
рисунок 2.2 |
|||
4 |
9 |
2 |
3 |
5 |
7 |
8 |
1 |
6 |
рисунок 2.1 |
||
Девять порядковых чисел размещены в девяти клетках квадрата так, что суммы чисел вдоль каждой строки, каждого столбца и каждой из двух диагоналей одинаковы (основное свойство магического квадрата).
Более поздние сведения о магических квадратах, относящиеся уже к I-веку, получены из Индии. Вот один из таких древнеиндийских памятников почти 2000-летней давности (рис 2.2):
Здесь 16 порядковых чисел расположены в шестнадцати клетках квадрата так, что выполняется основное свойство магического квадрата. Действительно:
1 + 14 + 15+ 4 = 34
12+ 7+ 6+ 9 = 34
8 + 11 + 10+ 5 = 34
13+ 2+ 3+16 = 34
1+7+10+16=34
13+11+6+4=34
Каждое число магического квадрата участвует в двух суммах, а числа, расположенные по диагоналям, даже в трех, и все эти суммы равны между собой.
Недаром в ту далекую эпоху суеверий индийцы, а следом за ними и арабы приписывали этим числовым сочетаниям таинственные и магические свойства.
Вся эта своеобразная мозаика чисел с ее постоянством сумм действительно придает магическому квадрату «волшебную» силу произведения искусства.
2.2 Магический квадрат у Гете.
И магические квадраты вошли в искусство.
В «Фаусте» Гете есть сцена приготовления колдуньей омолаживающего зелья. Слова, которыми колдунья сопровождает свои манипуляции, обычно воспринимаются читателями «Фауста» как тарабарщина, бессмыслица:
Du musst verstehen! |
…………………………… Пропускаешь 2, А также 3 Из 5 и 6 …………………………… делаешь 7 и 8 (и наоборот) |
Литературным критикам и не могло в голову прийти записать все это на бумаге. Давайте это сделаем. Построим квадрат из девяти ячеек и разместим в ячейках 9 первых натуральных чисел в порядке их следования. Выполним указания колдуньи:
Из 1 делаешь 10 — в первой ячейке заменяем число 1 числом 10. Числа 2 и 3 оставляем на своих местах, так как сказано: пропускаешь 2, а также 3.
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
рисунок 2.3 |
||
Зачеркиваешь 4 — это значит заменяем нулем число 4. Заменяем 5 и 6 числами 7 и 8, а в ячейки, занятые числами 7 и 8, вписываем 5 и 6 (рис 2.3 и 2.4):
Колдунья говорит: «Квадрат готов», но тут она хитрит. Ей еще надо в последней ячейке квадрата заменить девятку числом 4.
Особенность получившегося квадрата состоит в том, что магическая константа (15) получается только при сложении чисел вдоль любой строки и любого столбца, но не вдоль диагоналей. Квадрат с таким свойством чисел, занимающих его ячейки, принято называть полумагическим.
10 |
2 |
3 |
0 |
7 |
8 |
5 |
6 |
4 |
рисунок 2.4 |
||
10 |
2 |
3 |
0 |
7 |
8 |
5 |
6 |
9 |
рисунок 2.5 |
||
Превращением начального квадрата в полумагический Гете символизировал процесс омоложения Фауста.
2.3 Проникновение магических квадратов в Европу.
В Европу магические квадраты проникли лишь в начале XV века. А в начале XVI века один из них был увековечен выдающимся немецким художником, гравером и немного математиком А. Дюрером в его лучшей гравюре «Меланхолия» (1514 г.).
Дюрер воспроизвел на гравюре (в несколько измененном виде) тот самый магический квадрат, составленный из 16 чисел, который показан на рис 2.2.
Укажем еще шесть дополнительных свойств приведенного выше шестнадцатиклеточного магического квадрата:
- Сумма чисел, расположенных по углам нашего
магического квадрата, равна 34, то есть тому же числу,
что и сумма чисел вдоль каждого ряда квадрата. - Суммы чисел в каждом из маленьких квадратов
(в 4 клетки), примыкающих к вершинам данного квадрата, и в таком же центральном квадрате тоже одинаковы и каждая из них равна 34:
1+14+12+7=34
8+11+13+2=34
10+5+3+15=34
15+4+6+9=34
7+6+11+10=34
- В каждой его строке есть пара рядом стоящих чисел, сумма которых 15, и еще пара тоже рядом стоящих чисел, сумма которых 19.
- Подсчитаем сумму квадратов чисел отдельно в двух крайних строках и в двух средних:
12 +142+152+42=438 и 132 +22+32+162=438
122 +72+62+92=310 и 82 +112+102+52=310
Видно, что получились попарно равные суммы.
5. Нетрудно убедиться, что аналогичным свойством обладают и столбцы чисел. Суммы квадратов чисел двух крайних столбцов равны между собой, и суммы квадратов чисел двух средних столбцов тоже одинаковы.
6. Если в данный квадрат вписать еще один квадрат с вершинами в серединах сторон данного квадрата, получим то, что показано на рисунке 2.6 выше:
12 |
7 |
6 |
9 |
1 |
14 |
15 |
4 |
8 |
11 |
10 |
5 |
13 |
2 |
3 |
16 |
рисунок 2.7 |
|||
1 |
14 |
15 |
4 |
12 |
7 |
6 |
9 |
8 |
11 |
10 |
5 |
13 |
2 |
3 |
16 |
рисунок 2.6 |
|||
а) сумма чисел, расположенных вдоль одной пары противоположных
сторон вписанного квадрата, равна сумме чисел, расположенных вдоль другой пары противоположных его сторон, и каждая из этих сумм равна
опять-таки числу 34:
12 + 14 + 3 + 5 = 15+9+8+2 = 34;
б) еще интереснее то, что равны между собой даже
суммы квадратов и суммы кубов этих чисел:
122 +142+32+52 = 152 +92+82+22
123 +143+33+53 = 153 +93+83+23
Если столбцы квадрата сделать его строками, сохраняя чередование, а
строки столбцами, то квадрат своих магических свойств не поменяет.
При обмене местами отдельных строк или столбцов магического квадрата некоторые из вышеперечисленных его свойств могут исчезнуть, но могут и все сохраниться и даже появиться новые. Например, поменяем местами первую и вторую строки данного квадрата, получим то, что показано на рисунке 2.7.
Суммы чисел вдоль строк и столбцов, конечно, не изменились, но суммы чисел вдоль диагоналей стали иными, не равными 34. Магический квадрат потерял часть своих основных свойств, стал «неполным» магическим квадратом (полумагическим квадратом).
Продолжая обменивать местами строки и столбцы квадрата, вы будете получать все новые и новые магические и полумагические квадраты из 16 чисел.
